こんにちは、えふです!
このページに辿り着いたあなたは、こんな悩みを持っていることでしょう。

2次関数の変域がよくわからない…。
正解できるときもあるんだけど…。



正解だと確信していたのに、なぜか間違っていた…!
ここでは、2次関数の変域についての問題を確実に正解するためのたった一つの方法について説明します!
この方法を実践してくれれば、上にあるような、「合っているときもあれば間違っているときもある」といったような不確実さをなくし、自信を持って回答することができるようになるでしょう!
それではさっそく見ていきましょう!
【10分でわかる!】変域を間違えずに求めるたった一つの方法
それでは、具体例を見てみましょう。
$y=x^2$ において、 $x$ の変域が $-1≦x≦3$ のときの $y$ の変域を求めなさい。
もしかして、こんな解き方をしていませんか…?
正しい解き方(?)



とりあえず、$x$ を式に代入して…
① $y=x^2$ に $x=-1$ を代入
$$y=x^2$$
$$y=(-1)^2$$
$$y=1$$
② $y=x^2$ に $x=3$ を代入
$$y=x^2$$
$$y=3^2$$
$$y=9$$



$1$ のほうが $9$ より小さいから、$1$ を左に、$9$ を右に書いて…
こうだ!
①, ②より $1≦y≦9$
これは危険!!!
答えも間違っています…。
このような解き方をしている人は、冒頭にあった「合っているときもあれば間違っているときもある」という症状に悩んでいるはずです。
「変域とはなにか」をしっかり理解して、確実に問題を解けるようにしていきましょう!
そもそも変域ってなに???
変域とは、その文字の値がいくつからいくつの範囲にあるのかを表したものです。
例えば「$-2≦x≦4$」 は、$x$ に当てはまる数が「 $-2$ 以上 $4$ 以下の数」であるということを表しています。
言い換えると、「$x$ は一番小さくて$-2$ で、一番大きくて $4$」ということです。
つまり、$x$ に当てはまる数は、例えば $-2$ , $-1.5$ , $-\frac{1}{3}$ , $0$ , $0.1$ , $\sqrt{2}$ , $\frac{3}{2}$ , $4$ などだということですね。
$x$ に制限がない場合は、少数でも分数でも無理数でもOKで、
$x$ に当てはまる数は無数にあるよ!
先ほどの問題は、口語にすると次のように表されます。
$y=x^2$ で、 $x$ が $-1≦x≦3$ の範囲で変化すると、それにともなって $y$ も変化するよ。では、$y$ は一番小さくていくつで、一番大きくていくつかな?



変域がどんなものかはわかってきたよ!



でも結局、代入はするんでしょう?
そうだね。
でも、その前にするべきことがあるよ!!
グラフを書こう!
2次関数の変域についての問題を確実に正解するためのたった一つの方法。
それは、グラフを書くことです!
たったそれだけ?と思ったかもしれませんが、これこそが変域を考える上で最も重要なことなのです。
では、グラフを確認しながらもう一度例題に取り組んでみましょう!
$y=x^2$ において、 $x$ の変域が $-1≦x≦3$ のときの $y$ の変域を求めなさい。



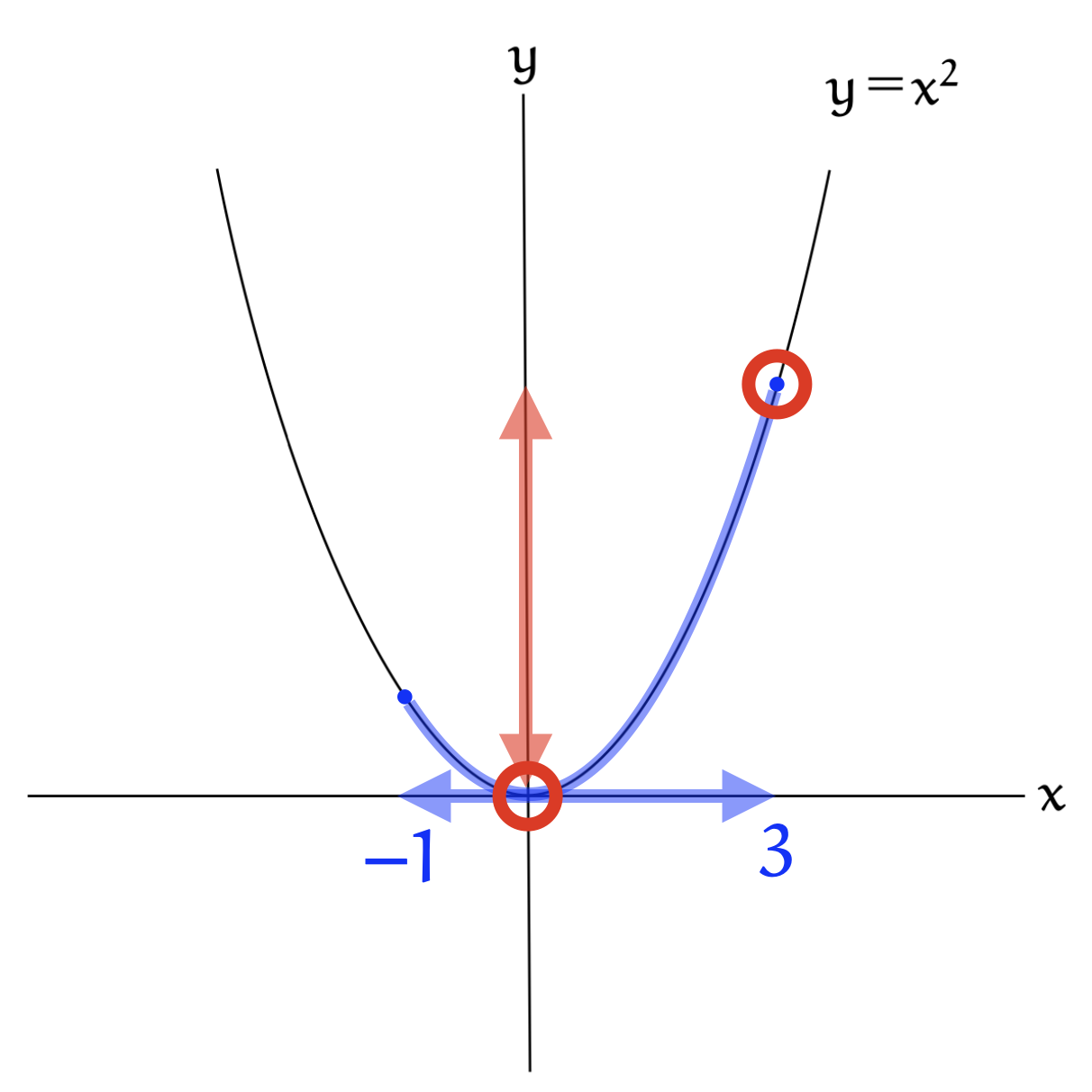
まずはグラフを考えよう。$y=x^2$ は上開きのグラフだから…
こんな感じかな!




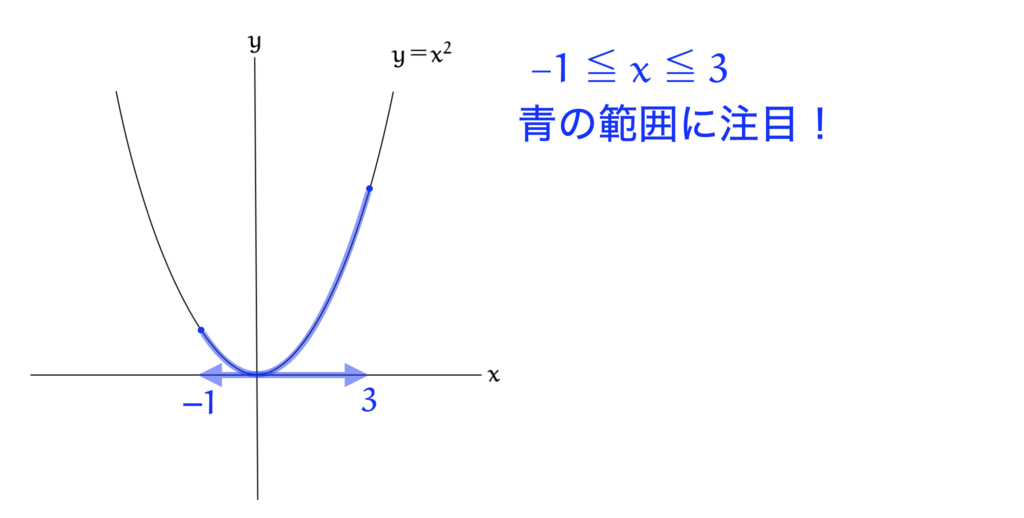
$x$ の変域が $-1≦x≦3$ だから、$-1$ と $3$ の間を見ればいいってことだね!




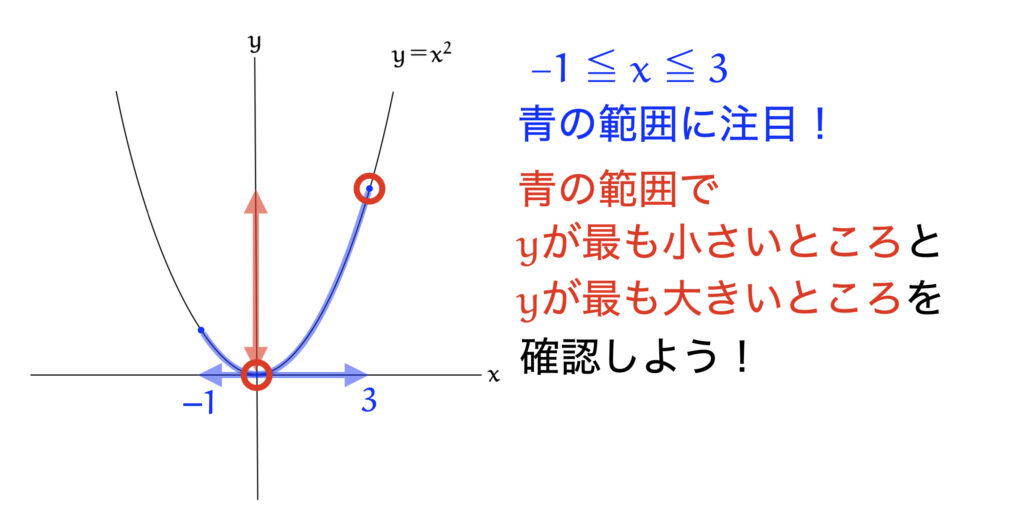
この範囲で、$y$ が一番小さいところと、$y$ が一番大きいところを探せばいいんだったね!

これで、$y$ の変域が求められそうだね!
正しい解き方



まずはグラフを書いて、大小を確認しよう!
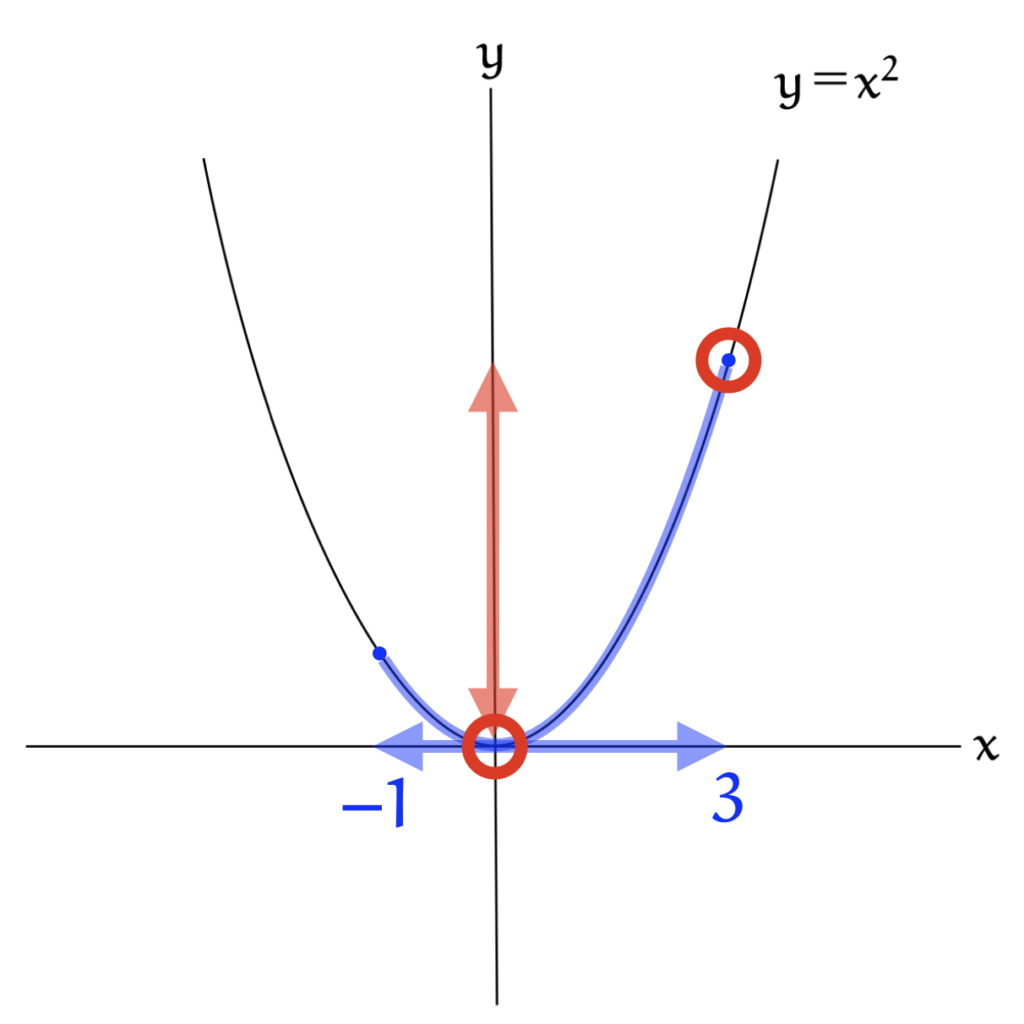

① グラフより 最小値は $y=0$
② グラフより $x=3$ で $y$ が最大となる
$y=x^2$ に $x=3$ を代入
$$y=x^2$$
$$y=3^2$$
$$y=9$$
①, ②より $0≦y≦9$
まとめ
関数の変域を求める問題で最も大切なことはグラフを書くことです!
今回は2次関数を例にとって話を進めてきましたが、比例や反比例、1次関数においてもまったく同じことが言えます。
特に、応用問題になってくると、グラフの形を確認することの重要性がより増します。
グラフとは、数値を図形にすることによって、その大小や変化をより理解しやすくするものです。
ぜひその力を借りて、さまざまな問題に挑戦していきましょう!
デカルトに感謝!

コメント